Semana # 34 y 35
Observa atentamente el siguiente vídeo, el cual te ilustrará sobre cómo hallar la fracción de una cantidad.
Semana # 32 y 33
Fracciones propias
Las fracciones propias son aquellas cuyo numerador es menor que el denominador. Su valor es menor que la unidad ya que se ubica entre cero y uno en la recta numérica.
Por ejemplo:
1 , 1 , 3 , 4 .
3 6 4 8
Al representar la fracción gráficamente tenemos:
Ejemplo:
Fracciones impropias
Las fracciones impropias son aquellas cuyo numerador es mayor que el denominador. Su valor es mayor que 1.
Al representar la fracción gráficamente tenemos:
Ejemplo:
Número mixto o Fracciones mixtas:
Las fracciones impropias se pueden escribir como numero mixto. El número mixto o fracción mixta está compuesto de un número entero y una fracción propia.
En el ejemplo anterior tenemos:
Semana # 31

Semana # 29
DESEMPEÑOS COGNITIVOS:
Identifica y selecciona apropiadamente elementos, acciones, conceptos y procesos matemáticos que le permiten responder de manera apropiada a las exigencias de la situación.
Comprende que escuchar la situación problema es fundamental para deducir colectivamente la tarea que se debe realizar.
Comprende apropiadamente que hay que retomar la lectura de la situación problema. Determinar la tarea que se debe realizar y el tipo de resultado esperado.
Encuentra de manera apropiada los conceptos y procesos matemático-requeridos para responder a las exigencias de la tarea.
Asocia apropiadamente una fracción a una colección de objetos.
Reconoce apropiadamente diferentes significados de un fraccionario. ( compartir, dividir).
Distingue apropiadamente el papel del numerador y del denominador.
Separa apropiadamente de manera equitativa un todo a partir de una fracción dada
Lee apropiadamente un fraccionario.
Verifica apropiadamente la equivalencia de dos fracciones.
Semana # 26 a la 28
Semana # 23 a la 25
Visualicemos el vídeo y comprende el proceso de la división.

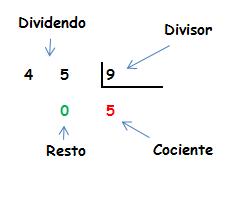
Los términos de la división son:
Dividendo: es el número que vamos a dividir.
Divisor: es el número por el que vamos a dividir.
Cociente: es el resultado.
Residuo: la parte que no se ha podido distribuir.
LIBRO DE MATEMÁTICAS
Semana # 21
n reloj es un dispositivo que permite realizar la medición del tiempo y segmentarlo en unidades (segundos, minutos, horas, etc.). El mecanismo del reloj consiste en desarrollar un movimiento de características uniformes, regulándolo con un péndulo. Dicho movimiento se comunica, a través de ruedas, con las agujas o manecillas que indican la hora.
Reloj analógico: estos indican la hora por medio de agujas que señalan la hora, minutos y segundos, apuntando a los números que se ubican a su alrededor y van del 1 al 12. La aguja que indica la hora es más ancha y corta que el minutero, que es más delgado y largo. Por último, el segundero, aguja que no siempre está presente, es la más delgada de las tres.
 Reloj digital: en este la hora se indica por medio de números digitales. Estos indican la hora, minutos y algunos, hasta los segundos y se pueden encontrar en dos formatos: 12 o 24 horas. En el de 12 horas se indica si estas son AM o PM.
Reloj digital: en este la hora se indica por medio de números digitales. Estos indican la hora, minutos y algunos, hasta los segundos y se pueden encontrar en dos formatos: 12 o 24 horas. En el de 12 horas se indica si estas son AM o PM.

Reloj de pulsera: estos dispositivos cuentan con una correa que se ajusta al ancho de la muñeca. Pueden ser analógicos, digitales o ambos.

Reloj de arena: por medio de este dispositivo mecánico se mide un transcurso de tiempo determinado, desde que la arena comienza a caer desde el receptáculo superior a inferior, hasta que termina. Actualmente, estos relojes han sido reemplazados por los cronómetros, que cumplen la misma función.


Semana #16 y 17
TABLA DE DATOS
Son las que organizan los datos para mostrar qué tan seguido ocurre algo (frecuencia), permite organizar la información numérica recogida, por ejemplo, a través de una encuesta.



Los gráficos permiten visualizar la información contenida en las tablas de manera rápida y sencilla, demostrando con mayor claridad la relación que estos datos tienen entre sí.

Semana # 14 y 15
Solucionemos problemas matemáticos.
Semana # 13
Semana # 12
Semana # 11

FIN DEL PRIMER PERIODO
semana # 10
Realiza las multiplicaciones en el cuaderno y colorea según el color de cada pista donde encuentres el resultado.

MULTIPLICACIÓN POR DOS CIFRAS
Observa con atención cada uno de los pasos, para que comprendas cómo se realizan este tipo de multiplicaciones.
Semana # 8

Semana # 6

Si faltas a clase, aquí puedes encontrar el taller del día 06-03-17
TALLER #3 DE MATEMATICAS
Semana # 5


Semana # 4

ACTIVIDAD EN CLASE
1. Representa en el ábaco y escribe el nombre de cada uno de los siguientes números:
A) 603.415
B) 502.849
C) 444415
D) 100249
E) 18402
COMPROMISO
Representa en el ábaco y escribe el nombre de los siguientes números:
Semana #3
Jueves 16 de febrero
ACTIVIDAD EN CASA
Pasa al cuaderno de matemáticas y resuelve:

EL VALOR POSICIONAL
FRACCIÓN DE UN NUMERO
Observa atentamente el siguiente vídeo, el cual te ilustrará sobre cómo hallar la fracción de una cantidad.
Semana # 32 y 33
FRACCIONES PROPIAS, IMPROPIAS Y MIXTAS
Las fracciones propias son aquellas cuyo numerador es menor que el denominador. Su valor es menor que la unidad ya que se ubica entre cero y uno en la recta numérica.
Por ejemplo:
1 , 1 , 3 , 4 .
3 6 4 8
Al representar la fracción gráficamente tenemos:
Ejemplo:
Fracciones impropias
Las fracciones impropias son aquellas cuyo numerador es mayor que el denominador. Su valor es mayor que 1.
Al representar la fracción gráficamente tenemos:
Ejemplo:
Número mixto o Fracciones mixtas:
Las fracciones impropias se pueden escribir como numero mixto. El número mixto o fracción mixta está compuesto de un número entero y una fracción propia.
En el ejemplo anterior tenemos:
Semana # 31
FRACCIONES EQUIVALENTES

Semana # 29
MATRIZ DE EVALUACIÓN DEL 4° PERIODO
DESEMPEÑOS COGNITIVOS:
Identifica y selecciona apropiadamente elementos, acciones, conceptos y procesos matemáticos que le permiten responder de manera apropiada a las exigencias de la situación.
Comprende que escuchar la situación problema es fundamental para deducir colectivamente la tarea que se debe realizar.
Comprende apropiadamente que hay que retomar la lectura de la situación problema. Determinar la tarea que se debe realizar y el tipo de resultado esperado.
Encuentra de manera apropiada los conceptos y procesos matemático-requeridos para responder a las exigencias de la tarea.
Asocia apropiadamente una fracción a una colección de objetos.
Reconoce apropiadamente diferentes significados de un fraccionario. ( compartir, dividir).
Distingue apropiadamente el papel del numerador y del denominador.
Separa apropiadamente de manera equitativa un todo a partir de una fracción dada
Lee apropiadamente un fraccionario.
Verifica apropiadamente la equivalencia de dos fracciones.
Semana # 26 a la 28
LOS NÚMEROS FRACCIONARIOS
Observa con atención el siguiente vídeo y participa con tu comentario en cuanto lo que entendiste en la discusión de la clase.
observa este otro vídeo espero se aclaren algunas dudas surgidas al rededor del tema a trabajar.
Semana # 23 a la 25
LA DIVISIÓN
La división se utiliza para repartir una cantidad en grupos iguales.
Por ejemplo:
Tenemos 45 bombones y queremos repartirlos entre 9 niños por lo que tenemos que formar 9 grupos con el mismo número de bombones.
Vamos a dividir 45 entre 9:

Los términos de la división son:
Dividendo: es el número que vamos a dividir.
Divisor: es el número por el que vamos a dividir.
Cociente: es el resultado.
Residuo: la parte que no se ha podido distribuir.

LIBRO DE MATEMÁTICAS
Semana # 21
¿QUÉ HORA ES?
Reloj analógico: estos indican la hora por medio de agujas que señalan la hora, minutos y segundos, apuntando a los números que se ubican a su alrededor y van del 1 al 12. La aguja que indica la hora es más ancha y corta que el minutero, que es más delgado y largo. Por último, el segundero, aguja que no siempre está presente, es la más delgada de las tres.


Reloj de pulsera: estos dispositivos cuentan con una correa que se ajusta al ancho de la muñeca. Pueden ser analógicos, digitales o ambos.

Reloj de arena: por medio de este dispositivo mecánico se mide un transcurso de tiempo determinado, desde que la arena comienza a caer desde el receptáculo superior a inferior, hasta que termina. Actualmente, estos relojes han sido reemplazados por los cronómetros, que cumplen la misma función.

APRENDAMOS A VER LA HORA

Semana #16 y 17
TABLA DE DATOS
¿Para qué nos sirven los gráficos y las tablas de datos?
Los gráficos y las tablas representan e interpretan información procedente de diferentes fuentes, de forma clara, precisa y ordenada. Casi todo tipos de información puede organizarse en una tabla de datos y ser representada en algún tipo de gráfico.
Según las características y la cantidad de datos, conviene utilizar uno u otro gráfico.
Tablas
Son las que organizan los datos para mostrar qué tan seguido ocurre algo (frecuencia), permite organizar la información numérica recogida, por ejemplo, a través de una encuesta.

Frecuencia : Tanto en las tablas como en los gráficos el número de veces que se repite un dato se denomina frecuencia de ese dato.
En la tabla se organizan todos los datos junto a las frecuencias que les corresponden.
Ej:
Ej:

En el gráfico o diagrama de barras, cada dato se representa mediante una barra cuya altura indica la frecuencia, es decir, cuantas veces se repite ese dato.
Ej:

Gráficos:
Los gráficos permiten visualizar la información contenida en las tablas de manera rápida y sencilla, demostrando con mayor claridad la relación que estos datos tienen entre sí.
Los más conocidos son:
Gráficos de barras: Son aquellos que emplean rectángulos (barras) que se colocan paralelamente. La altura indica la frecuencia de ese dato. Los gráficos de barras, permiten representar información numérica en forma clara y ordenada, para comunicarla a otras personas. Con la información representada en los gráficos puedes interpretar rápidamente y de manera visual la información, facilitando su posterior análisis.

Para construir un gráfico de barras, debes dibujar un eje vertical y otro horizontal. En el espacio libre se ubican las barra. Los datos numéricos van en el eje vertical (determinando la altura de las barras) y las categorías en el eje horizontal.
Semana # 14 y 15
Solucionemos problemas matemáticos.
Semana # 13
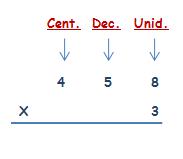
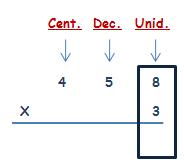
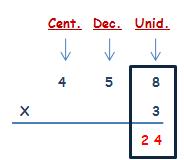
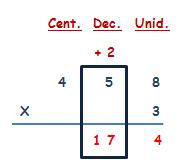
REPASEMOS LA MULTIPLICACIÓN POR 2 CIFRAS
SOLUCIONEMOS PROBLEMAS MATEMÁTICOS CON LAS OPERACIONES (suma - resta y multiplicación)
Está atento al vídeo, el cual te mostrará la manera más fácil para que aprendas la manera más practica de aprender a solucionar un problema matemático.
Semana # 12
ÁREA Y PERÍMETRO
Observa con atención el siguiente vídeo para que puedas comprender... qué es el área y como se calcula; igualmente el perímetro de figuras planas (cuadrado, rectángulos y triángulos).
Semana # 11
SIGAMOS MULTIPLICANDO
Realiza las multiplicaciones en el cuaderno y cuando obtengas los resultados, en el orden de las operaciones puedes ir armando el rompecabezas.

FIN DEL PRIMER PERIODO
semana # 10
ACTIVIDAD

MULTIPLICACIÓN POR DOS CIFRAS
Observa con atención cada uno de los pasos, para que comprendas cómo se realizan este tipo de multiplicaciones.
Semana # 8
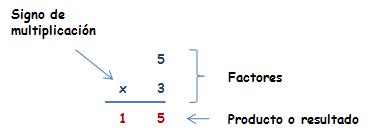
LA MULTIPLICACIÓN
Observemos el vídeo, para que comprendamos el concepto de multiplicar.

Semana # 6
SECUENCIAS GEOMÉTRICAS
según lo visualizado en el vídeo... determinar, ¿qué figura sigue para completar la secuencia geométrica?


Si faltas a clase, aquí puedes encontrar el taller del día 06-03-17
TALLER #3 DE MATEMATICAS
Semana # 5
SECUENCIAS NUMÉRICAS
(transcribe a tu cuaderno de matemáticas)
¿Qué es una serie numérica?
Una serie numérica es una secuencia de números ordenados, llamados términos, entre los cuales hay una relación que hay que descubrir, para completar la serie.
Por ejemplo, en la serie 0 - 7 - 14 - 21 existe una relación: el número 7. Esto quiere decir que para seguir la secuencia, solo debemos sumar el número 7 al último valor presentado, el 21.
Por ejemplo, en la serie 0 - 7 - 14 - 21 existe una relación: el número 7. Esto quiere decir que para seguir la secuencia, solo debemos sumar el número 7 al último valor presentado, el 21.

Para clarificar tus ideas, observa el siguiente vídeo.
ACTIVIDAD
En tu cuaderno realiza las siguientes secuencias numéricas:

LAS FIGURAS GEOMÉTRICAS
PROPIEDADES DE LOS NÚMEROS
Debemos representar los números según su valor posicional en el ábaco; como lo muestra la siguiente imagen.
ACTIVIDAD EN CLASE
1. Representa en el ábaco y escribe el nombre de cada uno de los siguientes números:
A) 603.415
B) 502.849
C) 444415
D) 100249
E) 18402
COMPROMISO
Representa en el ábaco y escribe el nombre de los siguientes números:
- 344.791
- 203.019
Semana #3
Jueves 16 de febrero
ACTIVIDAD EN CASA
Pasa al cuaderno de matemáticas y resuelve:

EL VALOR POSICIONAL
Observa el vídeo y si tienes dudas no olvides preguntarle a tu maestra.
realicemos el taller que la docente entregará en clases.





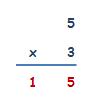



Buenos Dias Profesora Adriana Le Habla La Mamá De Valeria Bonilla Del Grado 3-1
ResponderEliminarUna Pregunta ¿Hasta Donde Se Trabaja Lo De Matematicas E Imprimimos Las Copias????